Tuesday, March 31, 2015
Exciting!
Getting ready to code for Save The Humans.
ref: Head First C#, 3rd edition, O'Reilly.
* * *
Some difficulty getting the Avoid These sign and the Extraterrestial dots on the same Stackpanel. For the moment, it looks like this:
Sunday, March 29, 2015
Caution Cont'd
Below the caution issue is explained. If I look at table data from Server Explorer, the original
database info has not changed. And if I run the project after that, it's back to the beginning...
database info has not changed. And if I run the project after that, it's back to the beginning...
BUT it works like a charm if I build and publish.
If I merely build:
The original database info cannot be changed from the app interface.
Difficulty!
Major Difficulty!! My Objectville program wouldn't persist changes to the data.
I added a try catch - like in the book - and am rewarded with a successful update
message, when it wasn't. Badddd!
* * * * *
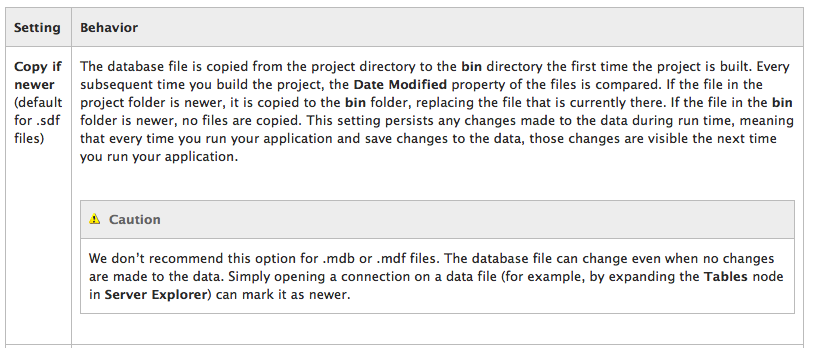
The solution seems to be changing the copy to directory settings:
I added a try catch - like in the book - and am rewarded with a successful update
message, when it wasn't. Badddd!
Obviously trying to go from boilerplate code to real, but this is a challenge.
* * * * *
The solution seems to be changing the copy to directory settings:
This approach comes with a caution, in effect about what might happen during
the development phase:
Thursday, March 26, 2015
DataAdapter
So one creates an SQL database, and fills it with information. One needs to establish a connection to it.
Tuesday, March 24, 2015
Learning
Still uncertain about the code for page two: adding the decimals after
rounding seems a route for complications.
Moving on to a new aspect of the app. Learning to mount a database on the
app for information storage.
https://youtu.be/l-fQVJAezGo
rounding seems a route for complications.
Moving on to a new aspect of the app. Learning to mount a database on the
app for information storage.
https://youtu.be/l-fQVJAezGo
Saturday, March 21, 2015
Friday, March 20, 2015
Testosterone!
March is the month for auto-immune diseases. People who
suffer from such diseases often know a great deal about their own disease,
for example diabetes 1, multiple sclerosis, lupus, Hashimoto, etc. But looking at all of these
as a whole can give insights, as well . In particular the fascinating fact that almost 80% of sufferers
are women! And that the occurrence of such diseases is linked to a deficit of testosterone.
Not something one hears about very often...
http://www.futura-sciences.com/magazines/sante/infos/actu/d/medecine-maladie-auto-immunes-10/
http://cirrie.buffalo.edu/encyclopedia/fr/article/118/
suffer from such diseases often know a great deal about their own disease,
for example diabetes 1, multiple sclerosis, lupus, Hashimoto, etc. But looking at all of these
as a whole can give insights, as well . In particular the fascinating fact that almost 80% of sufferers
are women! And that the occurrence of such diseases is linked to a deficit of testosterone.
Not something one hears about very often...
http://www.futura-sciences.com/magazines/sante/infos/actu/d/medecine-maladie-auto-immunes-10/
http://cirrie.buffalo.edu/encyclopedia/fr/article/118/
Tuesday, March 17, 2015
Monday, March 16, 2015
Cumulative
Coding for cumulative is trickier than it looks: all variables need to be given an initial value,but one has to keep the y at 0 outside the loop to get a true cumulative.
Sunday, March 15, 2015
Wondering
The numbers behave if one keeps in memory numbers of umteen decimals for calculations.
Wondering how I can identify the 12-series that yields 5.32$ form those nums.
Friday, March 13, 2015
Case(rate)
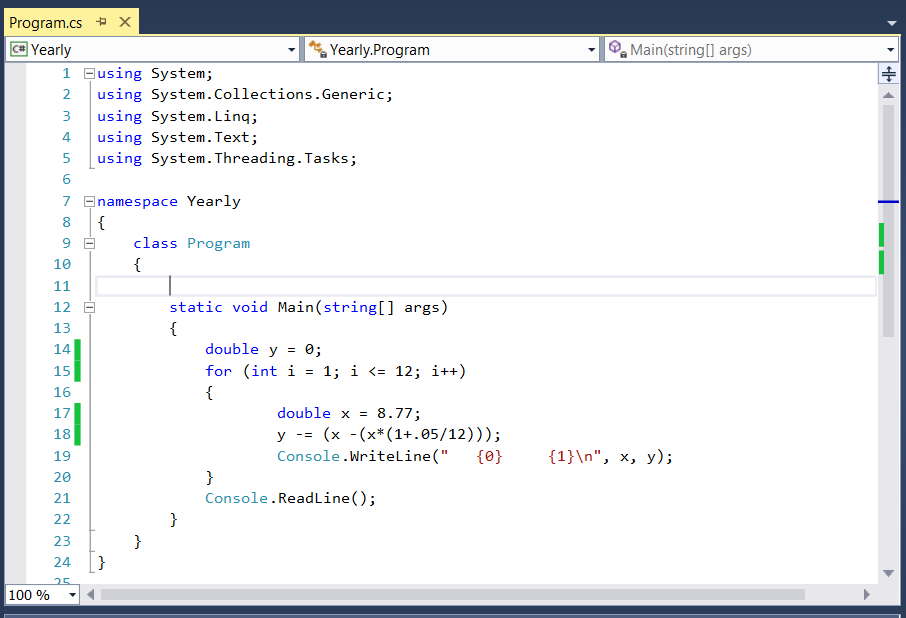
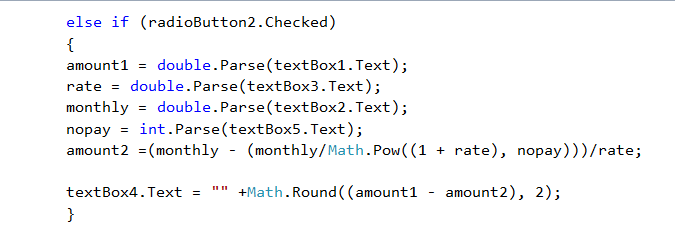
The first part of the Student Loan app is quite sane: looking into a loan situation from a clear perspective: how many payments would I have to make, how much would I still owe at time t.The second part is more of an after-the fact perspective. One is deep into it, and wondering when it will all end.
We will be considering two situations, working with, in both cases, amount of interest paid in one year, and amount of monthly payment
The two elements that give structure to a loan are: rate of interest, and number of payments. At the end of the day, interchangeable. Let us see what happens if we know interest rate.
With our example: I know that I have paid 5.32$ in interest in the last year, and made payments of 8.77$ per month. Adding to the mix that the interest rate was 5%, I will calculate for the interest amount for n =12. (Remember that the n(s) are moving backward in time from the point of view of amortization).
(1 - (1/1.004167^12))* 8.77 = .43
I then subtract the ln for power11, from ln power12, and convert to money, to get approximately .04.
This is the amount of change in interest payment from one month to the other. Now I need to locate the series which gives me 5.32$
Here is where the real programming begins; in pseudo-code:
-Create an array of 24
-Populate it with 4, 4+4, 4+ 4 + 4 etc
-Create a function that checks for a series of 12 that add up to 5.32
-Report the position in the array
Substract 1.That is how many payments of 8,77$ are still due.
Some programs give a balloon number at this point: how much is due if one merely pays
off the capital.
We will be considering two situations, working with, in both cases, amount of interest paid in one year, and amount of monthly payment
The two elements that give structure to a loan are: rate of interest, and number of payments. At the end of the day, interchangeable. Let us see what happens if we know interest rate.
With our example: I know that I have paid 5.32$ in interest in the last year, and made payments of 8.77$ per month. Adding to the mix that the interest rate was 5%, I will calculate for the interest amount for n =12. (Remember that the n(s) are moving backward in time from the point of view of amortization).
(1 - (1/1.004167^12))* 8.77 = .43
I then subtract the ln for power11, from ln power12, and convert to money, to get approximately .04.
This is the amount of change in interest payment from one month to the other. Now I need to locate the series which gives me 5.32$
Here is where the real programming begins; in pseudo-code:
-Create an array of 24
-Populate it with 4, 4+4, 4+ 4 + 4 etc
-Create a function that checks for a series of 12 that add up to 5.32
-Report the position in the array
Substract 1.That is how many payments of 8,77$ are still due.
Some programs give a balloon number at this point: how much is due if one merely pays
off the capital.
Thursday, March 12, 2015
Memory
For those with a Surface Pro, memory is very easy to use. Once one has put
something in M, one click will call it for use in calculations. One can add as many
M elements as one pleases. A right click on the letter M allows one to clear
all memory elements.
A screenshot can be taken with the Windows button down and a click on low sound.
A screenshot folder appears on the desktop.
Incomplete
Back to the incomplete information issue for our loan repayment app.:
We want to see if we can reconstruct the loan amount from interest paid over one
year and amount of payment. Let us create a simple situation of 100$ at 5% yearly repaid
in full over one year. Using our formula for payment:
p = .00417 * 100/(1 - (1/1.00417)^12)
= 8.57$
Multiplying by 12 we got, 102.81$
Can we reconstruct the loan payment, knowing we paid 2.81$ interest over one year. Of course; we merely solve for, in the above formula:
(p * 12) - 2.81 = PV
Now let's make things more complicated. We'll be working with a 200$ loan, at 5%, over two
years.Total repayment here totals 210.69$ with 10.69 interest. Alas, the bank sends us an enigmatic
tax paper to the effect that we have paid 5.32$ in interest last year. Looking at the amortization
schedule, this amount is the interest from the last six months of the first year and the first six of
the second.
Clearly, we are going to need more information...
We want to see if we can reconstruct the loan amount from interest paid over one
year and amount of payment. Let us create a simple situation of 100$ at 5% yearly repaid
in full over one year. Using our formula for payment:
p = .00417 * 100/(1 - (1/1.00417)^12)
= 8.57$
Multiplying by 12 we got, 102.81$
Can we reconstruct the loan payment, knowing we paid 2.81$ interest over one year. Of course; we merely solve for, in the above formula:
(p * 12) - 2.81 = PV
Now let's make things more complicated. We'll be working with a 200$ loan, at 5%, over two
years.Total repayment here totals 210.69$ with 10.69 interest. Alas, the bank sends us an enigmatic
tax paper to the effect that we have paid 5.32$ in interest last year. Looking at the amortization
schedule, this amount is the interest from the last six months of the first year and the first six of
the second.
Clearly, we are going to need more information...
New
If I had Anna Wintour's clothing allowance, I would be adding this little Phillip Lim number to
my wardrobe. Still, I purchased a new Joe Fresh winter sale sweater yesterday, feeling inspired.
Vivement le printemps!
Tuesday, March 10, 2015
Monday, March 9, 2015
Applying ln
How logarithms simplify life would be the following example. One needs to keep in mind that a logarithmic function stores information about something that has changed. One can read
on the graph how high the plane is at any time (the data). One can find the rate of climb as
a simple derivation. (Oh yes, this is Calculus!!)
on the graph how high the plane is at any time (the data). One can find the rate of climb as
a simple derivation. (Oh yes, this is Calculus!!)
http://www.intmath.com/differentiation-transcendental/7-applications-derivatives-log-exponential.php
Saturday, March 7, 2015
Those Exponents
Someone asked me how non-integer exponentials are calculated.
Like the joke says, very carefully. They are a difficulty and anyone with a new idea
on the subject will be listened to. Current best practice is to convert th exponent to
a fraction. Like 5^(5/11). Now it is obvious one wants to 5^5 first and then,
that result ^(1/11) or in the opposite order; the end result will be the same. And to
the question as to how one is supposed to find exponent (1/11), or the eleventh root of a number,
best practice there is to use natural logarithms.
ln(x)^(5/11) = 5/11 ln(x)
One finds ln(5), then one multiplies that number by 5, and divides by 11. Voilà.
Logarithms were invented to simplify calculations and this is how they do it.
ln(5) is worth 1.609437912...; * (3/11), gives .731562687...
e^.731562687... gives 2.078325845...
A calculator will verify this answer.
How were ln tables arrived at to begin with. By arduous calculation (leading eventually to the
invention of the slide rule). Newton devised an approximation method.
Interestingly, e itself can be found by (1 + 1/x)^x for the largest x one can imagine.
It is a limit. e is also given by
1 + 1/2 + 1/3 + 1/4 ...etc and not those abominable prime numbers. Whole numbers form the
ordinal series, and all of a sudden, everyone is worried about their mathematical properties.
Get a life!!
http://www.mathsisfun.com/algebra/exponent-fractional.html
Like the joke says, very carefully. They are a difficulty and anyone with a new idea
on the subject will be listened to. Current best practice is to convert th exponent to
a fraction. Like 5^(5/11). Now it is obvious one wants to 5^5 first and then,
that result ^(1/11) or in the opposite order; the end result will be the same. And to
the question as to how one is supposed to find exponent (1/11), or the eleventh root of a number,
best practice there is to use natural logarithms.
ln(x)^(5/11) = 5/11 ln(x)
One finds ln(5), then one multiplies that number by 5, and divides by 11. Voilà.
Logarithms were invented to simplify calculations and this is how they do it.
ln(5) is worth 1.609437912...; * (3/11), gives .731562687...
e^.731562687... gives 2.078325845...
A calculator will verify this answer.
How were ln tables arrived at to begin with. By arduous calculation (leading eventually to the
invention of the slide rule). Newton devised an approximation method.
Interestingly, e itself can be found by (1 + 1/x)^x for the largest x one can imagine.
It is a limit. e is also given by
1 + 1/2 + 1/3 + 1/4 ...etc and not those abominable prime numbers. Whole numbers form the
ordinal series, and all of a sudden, everyone is worried about their mathematical properties.
Get a life!!
http://www.mathsisfun.com/algebra/exponent-fractional.html
Friday, March 6, 2015
Reading Numbers
An interesting aspect of financial calculations is becoming familiar with
the formulas involved, effectively learning to 'read' them. What is the source
of the difficulty, giving us such apparently complex formulas? The quite simple fact
that .95 * 105 does not give 100. It gives 99.75. Because the reference number is now
larger than 100 ie 105. If I pay back ù 100$ at 5% after one year - 105$ - the percentage
of capital in the payment will be more than 95:
And the percentage of interest less than 5. For a loan being repaid monthly, this
situation will also hold.
1/1.0512 = the reciprocal; represents the capital part of payment
0.9513
1 - 0.9513
0.04867 the interest part of amount due for 1 month
The formula multiples the loan amount by the monthly interest rate, giving 4.17.
This is divided by the interest factor on the payment amount. The payment should be
85.68$ per month. (This should also be the last payment!!)
The first interest payment corresponds to a .0512 interest rate with respect to that
payment amount. The last - at 0.36 - to one of .0014617. One can check all those
in between using (1.004167)^11, (1.004167)^10 ... etc.
the formulas involved, effectively learning to 'read' them. What is the source
of the difficulty, giving us such apparently complex formulas? The quite simple fact
that .95 * 105 does not give 100. It gives 99.75. Because the reference number is now
larger than 100 ie 105. If I pay back ù 100$ at 5% after one year - 105$ - the percentage
of capital in the payment will be more than 95:
situation will also hold.
Working with the problem of a 1000$ loan at 5% repaid over one year, let's
examine the meaning of the numbers.
0.004167 5% over 12 months, per month
1.004167 a factor; adding interest to capital
(1.004167)^12 = above factor, iterated 12 times ( one year)
1.05121/1.0512 = the reciprocal; represents the capital part of payment
0.9513
1 - 0.9513
0.04867 the interest part of amount due for 1 month
The formula multiples the loan amount by the monthly interest rate, giving 4.17.
This is divided by the interest factor on the payment amount. The payment should be
85.68$ per month. (This should also be the last payment!!)
The first interest payment corresponds to a .0512 interest rate with respect to that
payment amount. The last - at 0.36 - to one of .0014617. One can check all those
in between using (1.004167)^11, (1.004167)^10 ... etc.
Thursday, March 5, 2015
S_Loan(Part2)
Moving on to the next utility in our Student Loan application. Let us say that
I receive a paper from the Bank, informing me that I have paid x amount in
interest on a loan in the taxation year; I remember that the interest rate
was 3% but little else. Can one reconstruct the rest of the situation.
As described, no. One can build scenarios that range from complete repayment, to payment of interest only, and many in-between. One needs one or more parameter: payment amount,
initial amount due, or end-of-the-year amount due. Here is the relevant formula.
P = r*(PV)/(1 - (1 + r)^-n)
monthly payment = rate*(initial amount)/(1-(1 + rate)^-(no of payments))
This formula would define, for a 1000$ loan at 5%, a monthly payment of
85.56$. Multiplied by 12, for a total of 1026.77$. The loan would have cost
26.77$. Here the transaction is complete after one year.
Had I remembered that I was making 50$ per month payments, use of the formula
would tell me I had paid 584.35$ in principal and 15.65$ in interest. Because I do
not know when payments will end, I cannot estimate the other parameters. I need
either beginning amount, or end-of-year amount to find the missing one.
I can create an app page for this situation.
I receive a paper from the Bank, informing me that I have paid x amount in
interest on a loan in the taxation year; I remember that the interest rate
was 3% but little else. Can one reconstruct the rest of the situation.
As described, no. One can build scenarios that range from complete repayment, to payment of interest only, and many in-between. One needs one or more parameter: payment amount,
initial amount due, or end-of-the-year amount due. Here is the relevant formula.
P = r*(PV)/(1 - (1 + r)^-n)
monthly payment = rate*(initial amount)/(1-(1 + rate)^-(no of payments))
This formula would define, for a 1000$ loan at 5%, a monthly payment of
85.56$. Multiplied by 12, for a total of 1026.77$. The loan would have cost
26.77$. Here the transaction is complete after one year.
Had I remembered that I was making 50$ per month payments, use of the formula
would tell me I had paid 584.35$ in principal and 15.65$ in interest. Because I do
not know when payments will end, I cannot estimate the other parameters. I need
either beginning amount, or end-of-year amount to find the missing one.
I can create an app page for this situation.
Tuesday, March 3, 2015
Subscribe to:
Comments (Atom)






.png)
.png)

%2B-%2BCopy.PNG)



%2B-%2BCopy.PNG)
%2B-%2BCopy.PNG)





.PNG)
.PNG)




R.PNG)


.png)




.PNG)
.PNG)



%2B-%2BCopy.PNG)



.PNG)
.png)
.png)