GNormal

The fact is well-known: the below formula and accompanying curve represent, in mathematics, the random distribution of probabilities or, in statistics, that of errors. All very nice, but what does that mean.

I cannot imagine a path of reasoning that would lead me to the median x at approximately 40%. With either an even or odd number of events, one is always dealing with 50-50 odds. Where does this number come from.

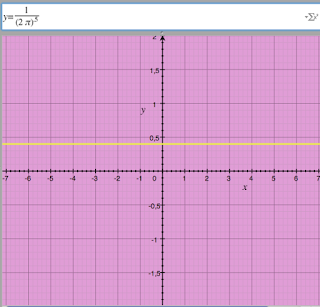
Looking at the simplest version of the formula - with the median at 0, and the standard deviation at 1(standard normal) - the coefficient of the function yields this .4. In effect, the probability of hitting the median position as such is 0. Every position is to be considered as a between of two others. In that world, one approximates the .4 at every turn. But why .4?

The quick answer: Pythagoras. the distance between two points is a square root, here of the full circle at 2 pi.The e part of the formula flips a classic exponential curve into a bell shape. (e is in fact necessary to avoid an asymptote at x=0). This function is a density representation. We half it and show positive and negative x.