For the description of movement in a 2 dimensional space, the orthonormal frame of reference is the Euclidien space: (0, 0) in the center, and graduated x and y axis.
Herein, any point c an be identified by its (x, y) address.
Indeed, one can specify movement within this space as changes in each of these two components.
Translation involves moving from one point to the other. And the linear journey between the two points i8s a vactor: a line with a length, direction, and orientation.
Defined in this manner, the vector is very useful: it can be reversed, added to or subtracted from, and scaled through multiplication.
* * *
My vector can be described as a (2, 2) vector, or as having a length of 2*(sqrt of 2).
And its multiplication by 2 would yield (4, 4) or a an absolute value of 4*(sqrt of 2).
Should I wish to do a multiplication of one vector by another, I would need to find the so-called dot product. ||A||*||B|| *cos(θ). That will give the effect of the new vector on the old, A on B. More simply I can consider the x, and y axis as carriers of i and j unit vectors. In this case, I multiply the i and j values of each vector with those of the other to get my new values.
sqrt8*sqrt5*.9484 = 6
2*2 + 2*1 = 6
The dot product is a value of considerable value in certain situations. Note
that, in the case where the angle is 0 degrees, the cosine value will be 1; and
in the case of 90 degrees, it will be 0. What this means is that the magnitude
of vector A will be a multiplier on B in the first case, and have no effect in the
second. Indeed, A can be anything!!
In a situation where one knows what the dot product is, on can easily find a
missing x or y value. If one has impact values, one can find the angle...etc







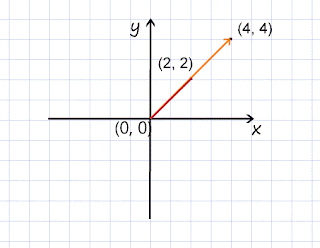


No comments:
Post a Comment