COPILOT:
Quantum Computing; what is an observable in quantum mechanics and what is in in quantum information theory?
In quantum mechanics, an observable is a physical quantity that can be measured, such as position, momentum, or energy. Mathematically, observables are represented by Hermitian operators acting on the state space of the quantum system. The eigenvalues of these operators correspond to the possible measurement outcomes, and the eigenvectors represent the states in which the system will be found upon measurement.
In quantum information theory, an observable retains its fundamental role as a measurable physical property. However, the focus is often on properties relevant to quantum information processing, such as qubit states and entanglement. Observables in this context are also represented by Hermitian operators, and they are used to extract information from quantum states, perform measurements, and analyze quantum algorithms.
quantum Information theory deals with on, off or spin up and spin down. What is the analog for that within physics?
In quantum information theory, the concepts of "on" and "off" or "spin up" and "spin down" correspond to the binary states of a qubit, which are typically represented as |0⟩ and |1⟩. These states are the quantum analogs of classical bits, which can be either 0 or 1.
In physics, particularly in quantum mechanics, these states can be represented by the spin of an electron or other particles. For example:
Spin Up (|↑⟩): This state can be associated with the qubit state |0⟩.
Spin Down (|↓⟩): This state can be associated with the qubit state |1⟩.
These spin states are fundamental in quantum mechanics and are used to describe the intrinsic angular momentum of particles. The superposition of these states allows qubits to exist in a combination of |0⟩ and |1⟩ simultaneously, enabling the powerful computational capabilities of quantum computers.
So the odds aren't always the same between these two states!!??
How is this simultaneous?
But these is only one statevector at any one time...
You're right! At any given moment, a qubit is described by a single state vector, which represents its superposition of states. This state vector encapsulates all the information about the probabilities and phases of the qubit being in the |0⟩ or |1⟩ state.
The state vector is a linear combination of the basis states |0⟩ and |1⟩, and it evolves according to the principles of quantum mechanics. When we measure the qubit, the state vector collapses to one of the basis states, and we observe a definite outcome (either |0⟩ or |1⟩). However, until the measurement is made, the qubit exists in a superposition, described by the state vector.
So, while there is only one state vector at any given time, this vector represents a superposition of multiple possible states, allowing the qubit to explore many possibilities simultaneously.
How can quantum computing claim running a large number of states simultaneously?
Great question! Quantum computing leverages the principles of superposition and entanglement to process a vast number of states simultaneously. Here's how it works:
Superposition: A qubit can exist in a superposition of both |0⟩ and |1⟩ states. This means that instead of being in a definite state, a qubit can be in a combination of states. For example, a single qubit in superposition can represent both 0 and 1 at the same time.
Entanglement: When qubits become entangled, the state of one qubit becomes dependent on the state of another, no matter the distance between them. This creates a complex, interconnected system where the state of the entire system cannot be described independently of each qubit.
Parallelism: Due to superposition and entanglement, a quantum computer can process multiple possibilities simultaneously. For example, with 𝑛 qubits, a quantum computer can represent 2^𝑛 different states at once. This exponential growth allows quantum computers to perform many calculations in parallel, vastly increasing their computational power.
Interference: Quantum algorithms use interference to amplify the probability of correct solutions and diminish the probability of incorrect ones. By carefully designing the quantum circuit, constructive interference enhances the likelihood of measuring the optimal solution.
So, while a qubit is described by a single state vector at any given time, this state vector represents a superposition of multiple states, allowing quantum computers to explore many possibilities simultaneously and solve certain problems more efficiently than classical computers.
And every time we do a shot, a different statevector is at play!!??
Yes, exactly! Each time you perform a measurement (or "shot") on a quantum system, the state vector collapses to one of the possible basis states (e.g., |0⟩ or |1⟩ for a single qubit) based on the probabilities defined by the superposition. After each measurement, the system is reset to its initial state or a new state, and the process can be repeated.
In quantum computing, running multiple shots allows you to gather statistics about the outcomes. By performing many measurements, you can estimate the probabilities of different states and gain insights into the behavior of the quantum system. Each shot provides a snapshot of the state vector at the moment of measurement, and the results can vary due to the probabilistic nature of quantum mechanics.
If qubit1 has a hadamard gate, is its statevector at every shot 50/50?
Consequently, on a simulator set to ideal states, there should be a 50/50 beakdown on each shot?
Yes, exactly! On a simulator set to ideal conditions, when a Hadamard gate is applied to a qubit initially in the |0⟩ state, each shot should result in a 50/50 breakdown between the |0⟩ and |1⟩ states. This is because the Hadamard gate creates an equal superposition of the two states, giving each an equal probability of 50%.
If you run multiple shots, you should observe approximately half of the measurements resulting in |0⟩ and the other half in |1⟩, reflecting the equal probabilities.
* * *
The mathematics of Statevectors is thus straightforward. My two
competing elements, |1> and |0> are in a Pythagorian relationship,
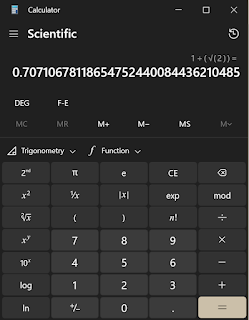
on the unit circle. For a qubit with a Hadamard gate, the amplitude
of each is 1/2^.5 or .7071. What is the probability for either of showing
up on measurement is .7071^2, which is .5...
On a strict pythagorean basis, each of two equal amplitudes could be expressed
as 1/2^.5:
As probabilities on 1, this becomes:
.8 and .6 would play out at .64 and .36, also equal to 1.
Good to remember that one is on the trigonometric circle. Adding the two amplitude
values straight up will gives values on a curve. (It's a circle, but our frame of reference
on it is fixed).
The python code for this was generated by COPILOT:










.PNG)
.PNG)
.PNG)

.PNG)
.PNG)




.PNG)
.PNG)
.PNG)
.PNG)
.PNG)


.PNG)
.PNG)
.PNG)
.PNG)
.PNG)

.png)
.png)
.png)








.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)