Fourier Series def, from Meta:
Got a helpful reference from Copilot, this morning, in reference to the math on
Fouries series and the transform:
The Fourier Transform and Its Math Explained From Scratch - Programmathically
The Fourier Transform:
* * *I know that integrals seem daunting. I fully understand the difference between the
length of a fence and the area of a yard, because there are units!!. With integrals,
one ends up conjecturing speeding cars, filling fish tanks and the like. Essentially,
we are changing the 'space'...
* * *
RECAP on Calculus:
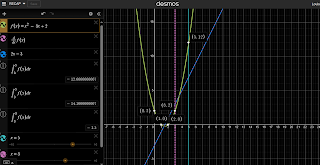
My example: In the first five days of October, leave have started to fall, at an increasing
pace every day. The parc at the corner is accumulating orange leaf bags. My leaf-o-meter
tells me that this equation describes the situation:
f(x) = x^2 - 3x + 2
How fast is this rate of accumulation increasing? I need to take the derivative to find out:
d/dx f(x) = 2x - 3
or f'(x) = 2x - 3
How many bags of leaves are there on the ground for any one day, or sequence of days.
The integral holds the answer:
f(x) = x^2 - 3x + 2
∫f(x) = 1/3 x^3 - 3/2 x^2 + 2x + C
* * *
Looking at the numbers, we can see the formula is a good soldier, and calculated
the negative entry in giving the 0 to 5 entry. Some of the leaves blew away during
day1 to day 2.
There is another possible scenario. We are putting our leaves in orange bags at the end of
each day, and none ever just disappear. Here we would have to calculate just the periods
with positive inflow and add them up.



No comments:
Post a Comment