Oh Noes!

http://www.wired.com/2015/05/will-computers-redefine-roots-math/

Lemma

The last Dimensions movie is a proof, which is straightforward enough: it rests
entirely on Euclid's Elements, in particular Pythagoras'Theorem and Thales.
One interesting twist: it makes use of a lemma, which is an intermediate
finding or theorem, which needs to be established for the actual proof to proceed.

                                                                     *  *  *

What is to be proven: that stereographic projection (from the north pole of the sphere)
will transfer a circle image form the sphere to the ground plane. Here, B Riemann's
likeness.We are in the realm of Geometry, this says nothing about what happens
to the proportions within the image. The quite famous picture of Riemann has been
 modelled onto a sphere image. A quick look convinces one that projection incurs
its own  form of distortion. Earth maps cannot compensate for this inescapable reality;
whatever projection model one chooses, the original longitude and latitude remain to
give the viewer a sense of what is going on.

*  *  *

Cutting s sphere creates a circle.

 Everything on the circle belongs to the sphere.

That sphere can be continued to a cone.

(Our lemma) ... which is symmetrical.

Every projection traces a circle.

 That projection can be carried to the South Plane.

We are now familiar with Riemann's Sphere.

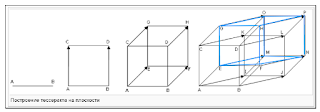
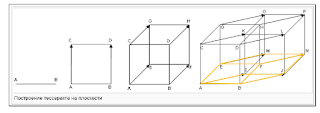
Tesseract

What is a cube in 3-D space becomes a tesseract (8 cubes) in 4-D. Every point

is called upon 4 times.

 

 

Russian-language Wikipedia.

4-D

*  *  *

Heavy!

My current forays into the history of Mathematics brought back to me the memory of
Euclid's Elements, one of my fondest moments from High School ( the worst was
Biology which I dropped for Physics; Save the Frogs!). I thoroughly enjoyed all the
problems but, as I recall, the introduction to the work was awesome and somewhat
mysterious. Let us look again at the Axioms and Postulates:

Today, both concepts are defined as self-evident truths but what is the difference 

between them. The clue to the issue comes from Aristotle, in whose work on 

Logic the Organon, axioms are referred to as primary notions with which one 

builds demonstrations. Postulates, in turn, define the field of study: it comes from 

asking for, here a line, a point, a circle, parallels. The statement of the fifth postulate is 

cleverly presented, ie those lines where angle deviation from the parallel

will be on the same side. Euclid comes a bit later than Aristotle, but his influence 

here is clear as well. He thought that logical connections came from experience 

itself,  whose richness informed the mind, because there was just too much otherwise.

Interestingly, the followers of Aristotle quickly came to the view that he had been 

right, and that all one needed to do was to understand him, a view that prevailed to 

the Renaissance. Ironic and misguided: philosophy is an acitvity. Plato knew that 

and Aristotle himself wrote on the dialectic. Perhaps it was the heaviness of the 

written word that came to prevail...

Math vs Logic

From the point of view of Mathematics, Russell's paradox has been
laid to rest through the Zermelo-Frankel Axioms(1920s) which constitute
the working  form of Set Theory. Below:

Number 7 prohibits X being an element of itself outright.


In 1960, the American mathematician Paul Cohen is deemed to have
shown that the axiom of choice is independent of the continuum hypothesis,
thus convincing the hold-outs that continuity and the axiom of choice are not linked.

From the point of view of Logic, Cohen's independence is in effect
undecidability.  An example of undecidability would  that parallel lines don't
meet with respect to Euclidian Geometry. One cannot decide whether this is
true or false from within Euclidian Geometry.

Plan d'Argand

Found a  mathematical resources site, especially good on the history of
Mathematics which is useful for making sense of things, and how they
are used.  On the history of Complex numbers, the plan d'Argand - adding
Geometry to the Cartesian plane -is really quite clever. As explained in Film 5
of the Dimensions series, once one has the courage to leave the numbers line,
and express things using i, the figures formed can be used to compute
using vector-like computational techniques. (Vectors themselves will come later,
because as well as a orientation and magnitude, a proper vector has a direction).

Euler eventually adopted the Argand plane as well. Euler's Formula states that any

real number can be expressed on this plane. Indeed it can,  because in Polar
notation, the coefficient of pi makes one jump back and forth on the line, while
the r value is the modulus ie the magnitude.

An interesting aside, the idea of the complex number plane was first put 

forward by John Wallis in the 17th Century. He taught Geometry at Oxford 

University at a time when Oliver Cromwell was Chancellor (De Algbra 

Tractacus, 1685).

http://serge.mehl.free.fr/chrono/Argand.html

Legendre

 

 

 

Found this wonderful Labor of Love rendition of famous mathematicians

on the Net. I was particularly pleased with the rendition of Adrien Legendre,

who has come down to us with only a disheartening caricature. I was trying

to imagine the face the artist had mocked. Done and awesomely

so!

 

 

 

 

http://angelustenebrae.livejournal.com/

Topology

http://www.infoplease.com/encyclopedia/science/topology.html

http://www.dimensions-math.org/Dim_E.htm

Lagrange Points

Newton's heritage left many unanswered problems, which he himself foresaw.

The three body problem in mathematics - finding the relative position of three bodies under mutual gravitational attraction - has no analytic solution. That is because those positions never form a repeating pattern; there is something that changes all the time. We are left with at best  a series of approximations.

The mathematician Lagrange (and others after him) looked at it another way. He defined identifiable points of equilibrium of forces between two large bodies that a third of negligeable mass could inhabit. In effect, he found points where the third object would follow along with the second in its orbital movement.This is the basis on which we today position observational devices such as  the future James Webb telescope at Lagrange 2.

The German Wikipedia points out that, for Earth, Lagrange 2 is 1/100 the length of the distance between the Sun and Earth: (gravity being a function  of mass and the square of distance , voir Newton). 

Not all the Lagrange points are arrived at in the same manner, and mathematically there is a great deal going on. Newtonian mechanics applies to two bodies in an inertial system ie one that does not move; however, a planetary system does move, and one needs to take centrifugal forces into account (Coriolis). Long story short, the L1 and L2 points are not stable, and this is what we want, because they will not accumulate planetary litter the way other points will. It has estimated that there are some 5 000 planetoids at Lagrange 4 and 5 for Jupiter (so-called Trojan planets). We can maintain an artificial satellite at L2 with a minimal expenditure of fuel.