Measurement

 Been trying to make sense of the measurement issue in Qiskit. Qiskit only

measures in the Z-basis, which - using 01 or10 -is the same as the classical on/off.

Below:

CHATGPT-4:

In quantum computing, the X-basis is a measurement basis that consists of the states |+⟩ and |−⟩. 

The state |+⟩ is often referred to as the "plus" state and is obtained by applying a Hadamard gate (H gate) to the |0⟩ state. Mathematically, the |+⟩ state is represented as:

|+⟩ = (|0⟩ + |1⟩) / √2

Similarly, the state |−⟩ is often referred to as the "minus" state and is obtained by applying a Hadamard gate to the |1⟩ state. Mathematically, the |−⟩ state is represented as:

|−⟩ = (|0⟩ - |1⟩) / √2

These states are orthogonal to each other:

⟨+|+⟩ = 1  

                                                                 *     *     *

In quantum computing, the Y-basis is another measurement basis that consists of two states: |i⟩ and |-i⟩. These states are defined in terms of the complex unit i (or sometimes denoted as j) where i^2 = -1.

The state |i⟩ is obtained by applying a Y gate (also known as the square root of Z gate) to the |0⟩ state, and the state |-i⟩ is obtained by applying the Y gate to the |1⟩ state. Mathematically, the |i⟩ and |-i⟩ states are represented as:

|i⟩ = (|0⟩ + i|1⟩) / √2  

|-i⟩ = (|0⟩ - i|1⟩) / √2  

Similar to the X-basis, the Y-basis states |i⟩ and |-i⟩ are orthogonal to each other:

⟨i|i⟩ = 1  

⟨-i|-i⟩ = 1  

⟨i|-i⟩ = 0  

When performing measurements in the Y-basis, the quantum system is projected onto either the |i⟩ state or the |-i⟩ state. The probability of the system collapsing into one of these states upon measurement is determined by the inner product of the current quantum state with the basis states |i⟩ and |-i⟩.

Measuring in the Y-basis provides a different perspective on the quantum state of a system and is useful in various quantum algorithms and quantum information processing tasks.

⟨-|-⟩ = 1  

⟨+|-⟩ = 0  

The states |+⟩ and |−⟩ form a basis known as the X-basis, which is commonly used in quantum computations. Measurements in the X-basis are commonly used in quantum algorithms and quantum circuits.

                                                                           *     *     *

In Qiskit, when it's said that measurement is only allowed in the Z basis, it means that the quantum circuit can only measure the qubits in the computational basis (i.e., the basis spanned by |0> and |1>).

In other words, Qiskit's measurement operation is defined to project the qubits onto the Z axis, which corresponds to the computational basis. This means that the measurement outcome will always be either |0> or |1>, which corresponds to the classical bits 0 and 1.

This is in contrast to measuring in the X basis (|+> and |->) or Y basis (|i> and |-i>), which would project the qubits onto different axes and potentially yield different measurement outcomes.

By only allowing measurement in the Z basis, Qiskit is effectively restricting the measurement to the classical bits 0 and 1, which is useful for most quantum algorithms and applications. However, some advanced quantum information processing tasks may require measurement in other bases, which would require additional processing or modifications to the quantum circuit.

Let me know if you have any other questions!

                                                                  *     *     *

META:

In Qiskit, measurements are indeed done in the Z-basis by default. To measure in a different basis, you need to apply the appropriate rotation gates before measurement.

To measure in the X-basis, you would need to apply a Hadamard gate (H) before measurement, not an X-gate. The Hadamard gate rotates the qubit to the X-basis, allowing you to measure in that basis.

Here's an example:

qc.measure_range(0, len(qr), qr)

Becomes:

Python

qc.h(qr)

qc.measure_range(0, len(qr), qr)

This applies a Hadamard gate to each qubit in the quantum register qr before measurement.

Note that if you want to measure in the Y-basis, you would need to apply a rotation gate RY(π/2) before measurement.

I hope that helps! Let me know if you have any further questions.

                                                            *     *     *

To measure in the Z-basis, you don't need to apply any additional gates! The Z-basis is the default measurement basis in Qiskit, so you can simply end your circuit with a measurement instruction, like this:

Python

qc.measure(qr, cr)

This will measure the qubits in the quantum register qr and store the results in the classical register cr, in the Z-basis.

So, to summarize: no extra gate is needed to measure in the Z-basis. Just end your circuit with a measurement instruction, and you're good to go!

                                                   *     *     *

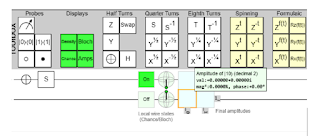
Managed to get a phase angle reading out:

                                                     

That's pi/2!!

Here it is in Quantum Composer:

                                                                          

From Quirk:

                                                                          

Including the complex value:

                                                                    

Gemini provided help with the code...