Subroutine

 Complexity Theory, as applied to Quantum Computing, is  serious business. As an

initiatee to the field, suffice it to appreciate that Big O notation allows one to undertand

that polynomial operations, like addition at O(n), are most cost (or time) effective. Moving

on to multiplication and division, we are looking at exponential values ie O(n^2), quadratic for 

Common Denominator, and cubic for modulus exponentiation O(n^3). Well, actually not.

All of these can be accomplished in polynomial time, by using a certain set of gates for

operations.

These gates are the NOT, CNOT and Toffoli...CCNOT. And by employing these judiciously,

one can run classical operations as subroutines in otherwise clearly quantum operations.

A Toffoli gate:

                                                                    

                                                                                       

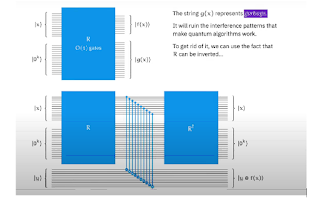
So the process involves creating ancillary bits on ket 0. The information from the original

input then gets transferred to what is now a quantum query gate. The intermediate operations

get erased, subsequently, by running the operation backward.