HA!

For today's math moment, would like to explore
(and eventually replicate) this graph of zeta values:

Those pink reals form a sideways parabola!!

So I googled the wrong thing, and ended up finding the solution 😄
Ended up with a whole song and dance on parabolas:

https://www.mathsisfun.com/geometry/parabola.html

And, on the solving quadratics page, got useful information about the vertex.

Ha!

https://www.mathwarehouse.com/geometry/parabola/

http://www.clausentech.com/lchs/dclausen/algebra2/parabolas.htm

MSalad

This is my 10 am breakfast on a muggy day. It looks
like a lot but is my usual calorie allowance, around 250
calories. It is in fact, high fiber. I have mixed pineapple,
cantaloup and cucumber with 2% cottage cheese. On
lettuce (which is currently plentiful) with Ryvita crackers
and almond butter.

It fulfills my daily requirements for raw vegetables ie salad.

                                                                      *     *     *

It recently struck me how chagrin (sad) the whole discourse about

healthy eating has become. It is totally decontextualized and someone

with diet fatigue might end up eating Christmas cookies in July because

the points are good on Weight Watchers. Christmas is not in July, and

it - and its cookies - is something one looks forward to come Fall.

One of the most famous passages in French literature is Proust's treatment

of his hero eating a Madeleine (little butter tea cake), and being transported to 

a moment of his adolescence by the sea, surrounded by lovely girls. Human

memories are linked to sensory experiences. Who knew.

Read this morning about the dangers of intermitten fasting aka three

meals a day. Seems that the experience of hunger could lead to a rise

in cortisol. Indeed, it could. We evolved as animals meant to forage

and hunt for our sustenance, and the stress hormone cortisol is what

makes it possible for us to take action. Let's not get silly, here, and conflate

description and prescription.

Troll

A read through the Wolfram article on Riemann's zeta paper
reaasures me that my working formula is indeed the correct
one for the whole complex plane. And I am starting to see how
each computational chunk of it would need a lot of work to see
what is going on.

Looking at the uses of s at either end, they behave in opposition
for both s greater than 1 - the Euler zeta for reals - and for s between
0 and 1, thus fractions and possibly complex expressions. This reflects
Riemanns multiplication of the old zeta with the gamma functions
to form his new zeta. (Is this a troll from the 19th century!?)

*     *     *

Not really complicated numerically, the first term is worth 2

for s at 2, and -5/2 for s at .5. It is a constant which can be

considered at each turn of fraction summation conceptually, but 

stated outside as a mathematical simplification.

The last term referencing s - as a funtion of k - is not a constant,

and will have a different effect with the different number of

iterations we ask for.

It is the work of the first term that shows the zeta is undefined

at 1.

*     *     *

Of more immediate concern, my transcription of the formula on
the (very useful) Desmos. It is clear that the fractions summation -
if we are careful about the zero value - goes to 1. And one is
tempted to dismiss the expression. THAT WOULD BE A SERIOUS
MISTAKE! In point of fact, it is never 1. And since we are looking
for zero coincidences...

The (-1) oscillation produces some zero factors, in its sums.

The binomial expression plays out entirely as a function the
n value we assign.

🙀

Hot Days

I have resisted getting ac unit, to date. A silly thing to
own, for a Canadian. Although we have been seeing some
hot days and nights, of late. Also read last week that the
blistering heat experienced in Europe was going toward Groenland,
so that means more melting ice and higher seas for us!

Declared today a McDay in the food department, and had
a shake for breakfast so far. The plan:

Ingredients:

Ice
2% milk
grapefruit juice
canned pineapple
cantaloupe
frozen (to ice) Astro lime yogurt

Comes in at under 300 calories, and not too sweet. The
experts tell us, actual ice cream is a false friend in hot
weather because sugar raises body temperature. This was
more like an Indian Lassi.

Made myself a Filet'O late afternoon, with tempura haddock and

cheese slice mozzarella. Was very nice, with a side of assorted veggies.

Interesting fact; fish is expensive and I could have bought the sandwich

at the restaurant for the what it cost me to make it...

Followed by dessert:

Last Meal, fries. These look large. Off to bed with my laptop and tray.

Tomorrow is a return to bananas!

Postscriptum

Day 2, and another very hot day. Made a bowl of fruit salad which I will

be aportionning over the day, probably between breakfast and lunch.

There is also a bowl of celery in water in the fridge, so the rice dish for

my main meal will be celery-heavy, something like in my childhood

when people only grocery-shopped once a week and we ate from what we 

had on hand.

I'm such a boo-ma!

Today's Problem

https://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%9A%D0%B0%D1%80%D0%B4%D0%B0%D0%BD%D0%BE

                                                           *     *     *

The original foray into complex numbers - by the Renaissance
Italian mathematician Cardano - was in aid of finding the roots
of cubic equations, a daunting practical task at the time.  In effect,
it was impossible to tell if any said equation had positive roots
without applying his formula. This will take some unraveling...
                                                                 *     *     *
First, let us recall how to evaluate a higher order sum, with a familiar
formula. It has a name,  the Binomial Theorem:

*     *     *

Next, we need to look at a modern formula which solves the simplest

higher order equation, the quadratic.

For (ax^2 + bx +c = 0):

The quadratic formula is actually a piece of reverse engineering,
ie from a buit-up construct, going in reverse to find the elements.
René Descartes was the first to use it, but could one derive the logic
behind it from the usual protocol used to solve quadratics?

Let's look at an example.
(x+2)(x+7)=
 x^2 + 9x + 14    which is:
ax^2 + bx + c      with a=1; b=9; and c=14.

What is the first thing I woud do, if asked to solve the equation?

I would ask myself what the possible factorizations of 14
is adequate to balancing the coefficients:
(b^2 - 2^2ac)^.5 = 5

How does it look with respect to b, given the play of signs?
-b + or - (b^2 - 2^2ac)^.5 = -4, -14

a here is 1, so there are two single x creating factors to account for:
-b + or - (b^2 - 2^2ac)^.5 /2a= -2, -7

Solving for zeros:
x - 2 = 0; x = 2
x - 7 = 0; x = 7
2 and 7 are then the roots of the equation.

An actual mathematical derivation of the formula - and
there are many - can be had on Wikipedia.

                                     *     *     *

If quadratics were easy enough to sole by intuition, or trial
and error, cubic equations were harder. Moreover, the fact
that one might face an equation with no actual roots could
not be ignored indefinitely. Cardan first published on a
systematic approach to some cubics. Bombelli then tackled
the issue of imaginary numbers, and how to use mathematical
operations on them.

Below, a change of constant term shows the funtion crosses
at 2 and -2.

Complex Ns

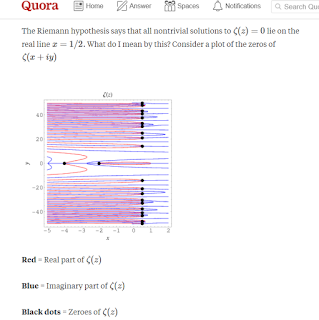
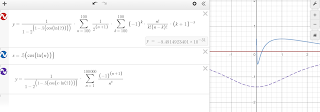
When I first learned about the complex plane,

it seemed a bit shocking to find e - the exponential, with

value2.78... - was leading something of a double life. Here

was the Euler identity, e^ipi +1 = 0, which clearly had little

to do with the value of either e or pi.


It is good to keep in mind that complex numbers developed

in the 16th century, as an aid to calculation. Should

you ask what the root(s) to 1^3 are, the answer has to

be 1, -1, -1. Otherwise the situation is confused because

a square root can be + or -. Can -1 have a square root? Yes, it can.

This is where e comes in.


I am putting a link to the Math is Fun page on complex mutiplication

below, but the gist is this: The real and imaginary terms on the

complex plane - cosine and sine of the unit circle - end up, through the

vagaries of computation,  playing different roles in complex multiplication.

When expressed in polar form, The real terms are multiplied to reflect magnitude, but

the angles are added and provide the angular movement. Indeed, every multiplication by i

represents a pi/2 counterclockwise shift. Works when an initial expression

is squared, or raised to the n (deMoivre' theorem).


Then in the 18th century, e gets used as the placehoder in the expression

e^i*pi- (e^Re(0)?) - with a shorthand complex exponent which is actually, (a + bi).

Does the presence of e change things? Yes, but in an unexpected way:

e^i gets evaluated as (cos(1) + i*sin(1)), the (understood) 1 being 1 rad.

e^(i*2) becomes (cos(2) + i*sin(2))...One can still identify the ln that

corresponds to that .54030 cos figure ( it is -.6156...) and do e-based

calculations .

(The use of i for (-1)^.5 was Euler's work. He went on to prove that the

square root of negative numbers can be expressed as multiples of i,

(-4)^.5 = 2*i.)


So when does e's value come into play. At e^(i)^2, i squared is -1; so

we are given e^-1, which is .3678. And of course, our (.5 + i) exponent

in the Riemann problen is treated as (e^.5)*(cos(1) + i*sin(1)).

                                                   *     *     *

https://www.mathsisfun.com/algebra/complex-number-multiply.html

http://villemin.gerard.free.fr/Wwwgvmm/Type/ImagComp.htm

Closing In

Working with the sign term, the first zero is very close to .

This means the cos term is close 0, of course.

                                                       *     *     *

https://www2.clarku.edu/faculty/djoyce/complex/

                                                       *     *     *

https://www.geogebra.org/m/yMWayZM7

Series

I knew from my own reasoning, but I googled
it anyway. Does 1/n^.5 form a convergent or divergent
series... It is divergent! Below, an interesting page from
Dummies on the question of p-series. (In French, these are
called Riemann series).

https://www.dummies.com/education/math/calculus/how-to-recognize-a-p-series/

From the Wikipedia entry on mathematical series:

For a long time, the idea that such a potentially infinite summation could produce a finite result was considered paradoxical. This paradox was resolved using the concept of a limit during the 19th century. Zeno's paradox of Achilles and the tortoise illustrates this counterintuitive property of infinite sums: Achilles runs after a tortoise, but when he reaches the position of the tortoise at the beginning of the race, the tortoise has reached a second position; when he reaches this second position, the tortoise is at a third position, and so on. Zeno concluded that Achilles could never reach the tortoise, and thus that movement does not exist. Zeno divided the race into infinitely many sub-races, each requiring a finite amount of time, so that the total time for Achilles to catch the tortoise is given by a series. The resolution of the paradox is that, although the series has an infinite number of terms, it has a finite sum, which gives the time necessary for Achilles to catch up with the tortoise.

From the French-language entry:

L'étude des séries à termes réels ou complexes, sans hypothèse particulière, peut poser plus de problèmes. Une condition suffisante a une grande importance : si la série des valeurs absolues (série à termes réels) ou des modules (séries à termes complexes) ${\displaystyle \sum \left|a_{n}\right|}$ converge, alors la série ${\displaystyle \sum a_{n}}$ converge également. Elle est alors dite absolument convergente.

Il existe des séries convergentes sans être absolument convergentes, comme la série harmonique alternée ${\displaystyle \sum {\frac {(-1)^{n}}{n}}}$. Les méthodes d'étude pour ce type de série, plus techniques, (critère de convergence des séries alternées, théorème d'Abel, …) sont présentées dans l'article détaillé Série convergente.

From the German:

And - helpful - the Russian:

Animation montrant la convergence des sommes partielles d'une progression géométrique (ligne rouge) à son montant(ligne bleue) avec . Avec Maple.

Hot

Heat extremes in Northern France, which is exceptional.

Cows have lost their usual appetite and have a quickened heartbeat.

source: Le Monde

That's 108.3 °F!

source: Libération

Dfferent

*     *     *

Time for me to try to reproduce what others are finding. Am thinking
of learning Géogebra but they only show the summation symbol on
spreadsheet iew. Very different!!