I am looking for 30).
The long way:
0^2 + 1^2 +2^2 + 3^2 + 4^2
= 0 + 1 + 4 + 9 + 16
= 30
Using Bernoulli formulas, I have three terms to add:
1/3 (n^3) - 1/2(n^2) + 1/6(n)
= 1/3(5^3) - 1/2(5^2) + 1/6(5)
= 125/3 -25/2 +5/6
= 250/6 - 75/6 + 5/6
= 180/6
= 30
Below, the well known Bernoulli numbers. They are, in effect, the last
coefficient from the lines in the formula table. The odd-numbered lines three and up are
listed as 0, because that is the value they evaluate to.
source: Wikipedia
* * *
To appreciate the computational models, one needs to be familiar with Pascal's
triangle.
Should I wish to calculate (a + b)^5 with it, I would go to line 6. The coefficients
go from left to right, with powers going down on a, and up on b.
Mathematically, one can find the coefficients within Pascal's triangle
by the following. These are the binomial coefficients:
source: Wikipedia
* * *



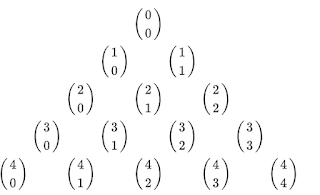

No comments:
Post a Comment