does one work with them? Bernoulli effectively arrived at
a new variety of Pascal's triangle, to enable one to add series of
natural numbers that have been squared. Each new B_number
multiplies a row on Pascal's triangle to create the S table.
Why and how does this work? Like the original Pascal's triangle, through
the magic of pre-determined combinations. If I square (a + b), I will
end up with 2ab as the second term of my answer, regardless of the
actual values of a or b. Here, if I add numbers to a given power x, a
first term n^(x +1) followed by a minus ... will be useful. The initial
insight for S(1) surprised me:
We are in the early 18th century - at the beginning of work on calculus -
and this shows up, one hundred years before Gauss,adolescent, famously
solved the sum of numbers up to 100 with n(n+1)/2. Bernoulli had a zero-
based term, but it is the same insight.
* * *
There is no plain n term in Sfor3. The Bernoulli number for that
column is zero.


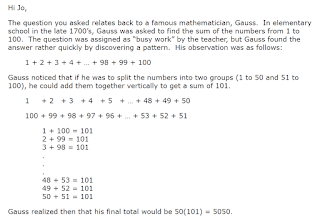


No comments:
Post a Comment