Quantum_Tech

 How do quantum computers work?

An IBM Quantum processor is a wafer not much bigger than the one found in a laptop. And a quantum hardware system is about the size of a car, made up mostly of cooling systems to keep the superconducting processor at its ultra-cold operational temperature.

A classical processor uses classical bits to perform its operations. A quantum computer uses qubits (CUE-bits) to run multidimensional quantum algorithms.

Superconductors

Your desktop computer likely uses a fan to get cold enough to work. Our quantum processors need to be very cold–about a hundredth of a degree above absolute zero—to avoid “decoherence,” or retain their quantum states. To achieve this, we use super-cooled superfluids. At these ultra-low temperatures certain materials exhibit an important quantum mechanical effect: electrons move through them without resistance. This makes them "superconductors."  

When electrons pass through superconductors they match up, forming "Cooper pairs." These pairs can carry a charge across barriers, or insulators, through a process known as quantum tunneling. Two superconductors placed on either side of an insulator form a Josephson junction.

Control

Our quantum computers use Josephson junctions as superconducting qubits. By firing microwave photons at these qubits, we can control their behavior and get them to hold, change and read out individual units of quantum information.

Superposition

A qubit itself isn't very useful. But it can perform an important trick: placing the quantum information it holds into a state of superposition, which represents a combination of all possible configurations of the qubit. Groups of qubits in superposition can create complex, multidimensional computational spaces. Complex problems can be represented in new ways in these spaces.

Entanglement

Quantum entanglement is an effect that correlates the behavior of two separate things. Physicists have found that when two qubits are entangled, changes to one qubit directly impact the other.

Interference

In an environment of entanged qubits placed into a state of superposition, there are waves of probabilities. These are the probabilities of the outcomes of a measurement of the system. These waves can build on each other when many of them peak at a particular outcome, or cancel each other out when peaks and troughs interact. These are both forms of interference.

A computation on a quantum computer works by preparing a superposition of all possibile computational states. A quantum circuit, prepared by the user, uses interference selectively on the components of the superposition according to an algorithm. Many possible outcomes are cancelled out through interference, while others are amplified. The amplified outcomes are the solutions to the computation.

                                       *     *     *

My second attempt on the Bromont computer:

                                       

                                                      *     *     *

From Bing/Chat:

The Heisenberg Uncertainty Principle significantly influences the behavior of electrons within atoms. Let’s explore how:

Orbital Position and Momentum:

Electrons in atoms occupy specific energy levels or orbitals around the nucleus.

The Heisenberg Uncertainty Principle implies that we cannot precisely determine both the position and momentum of an electron simultaneously.

As a result, we describe the electron’s position using a probability distribution (such as an orbital) rather than a fixed trajectory.

Quantum Numbers and Orbitals:

Quantum mechanics introduces a set of quantum numbers to describe the behavior of electrons:

Principal Quantum Number (n): Determines the main energy level (shell) of the electron.

Angular Momentum Quantum Number (l): Specifies the shape of the orbital (s, p, d, f).

Magnetic Quantum Number (m_l): Describes the orientation of the orbital in space.

Spin Quantum Number (m_s): Represents the electron’s spin (either +1/2 or -1/2).

These quantum numbers help define the allowed orbitals within an atom.

Uncertainty in Position and Energy Levels:

The uncertainty in position (due to the Heisenberg Uncertainty Principle) affects the size of the orbitals.

Larger orbitals (higher energy levels) have greater spatial uncertainty, allowing electrons to be farther from the nucleus.

Smaller orbitals (lower energy levels) have more localized positions.

Energy Levels and Stability:

Electrons occupy the lowest available energy levels (orbitals) first (following the Aufbau principle).

The uncertainty in momentum (related to energy) affects the stability of electrons.

Higher energy levels (with larger uncertainties) allow electrons to move more freely, contributing to the atom’s stability.

Quantum Mechanical Model of the Atom:

The quantum mechanical model describes electrons as wave functions (mathematical descriptions of their behavior).

Orbitals are regions of high probability density where electrons are likely to be found.

The shape of orbitals (spherical, dumbbell-shaped, etc.) arises from the Heisenberg Uncertainty Principle.

In summary, the Heisenberg Uncertainty Principle influences electron behavior by shaping the allowed orbitals, energy levels, and stability within atoms. It emphasizes the probabilistic nature of electron positions and their associated momentum. 🌌🔬

                                                       *     *     *

Certainly! Quantum tunneling is a fascinating phenomenon that occurs in the microscopic world of quantum mechanics. Let’s dive into the details:

1. Classical vs. Quantum View:

   • Imagine particles attempting to travel across a potential barrier, which is like a hill or an energy barrier.
   • In classical mechanics, if a particle doesn’t have enough energy to surmount the barrier, it cannot cross to the other side. It’s like a ball rolling back down the hill.
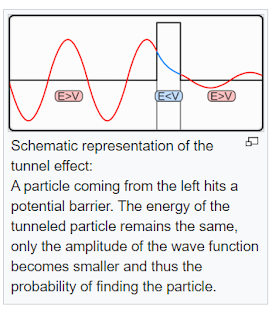
   • However, quantum mechanics introduces a different perspective. Even if a particle lacks sufficient energy, it can still tunnel through the barrier with a small probability.

2. The Tunneling Effect:

   • Quantum tunneling occurs when a particle (such as an electron) passes through a potential energy barrier that, according to classical physics, should be impossible to cross.
   • The particle behaves like a wave, and its wave function describes its state. The Schrödinger equation governs this behavior.
   • The probability of tunneling decreases exponentially with the barrier height, width, and the particle’s mass.
   • Low-mass particles (like electrons) can tunnel through microscopically narrow barriers.

3. Applications and Examples:

   • Nuclear Fusion: Quantum tunneling plays a crucial role in nuclear fusion reactions within stars and fusion experiments on Earth.
   • Alpha Radioactive Decay: Alpha particles (helium nuclei) tunnel out of atomic nuclei during decay.
   • Tunnel Diode: A semiconductor device that exploits tunneling for specific electronic applications.
   • Quantum Computing: Quantum bits (qubits) can tunnel between states, enabling quantum computation.
   • Flash Memory: Electrons tunnel through insulating layers in flash memory cells.
   • Scanning Tunneling Microscope (STM): Uses tunneling current to image surfaces at the atomic scale.

4. Detection and Limits:

   • We can detect tunneling when the barrier thickness is about 1–3 nm for electrons and even smaller for heavier particles like protons or hydrogen atoms.
     
     
     
     
   • In microelectronics, tunneling limits the minimum size of devices because electrons readily tunnel through thin insulating layers.

In summary, quantum tunneling defies classical intuition by allowing particles to pass through barriers they shouldn’t be able to cross. It’s a fundamental aspect of the quantum world and has practical applications in various technologies! 🌟🔬123