Theta

 Below, a succinct overview of phase kickback from someone

at Oxford University:

The takeway goes a long way in explaining why the Fourier basis is used for computation.

When something is between hadamard gates, one may not know the on/off state measurement

could yield, but the phase change is certain.

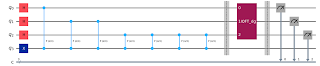
Below, the theta values for |0>, Hadamard, |1>

                                                               

*     *     *

Worked through thr e Sharma examplewhere one codes in at-gate and gets out

the value it represents, just to get a sense of the sequence. Going on next to Shor's

algorithm, one will be using phase estimation not knowing the answer beforehand...

Did learn something in the exercise, and that is optimization when going unto an

actualQuantum Computer. It can make all the difference.

                                                         

                                                                                   

I was getting two possible answers without optimization, and had to redo the run.

From Copilot:

When you transpile a quantum circuit in Qiskit before running it on an actual quantum computer, the `optimization_level` parameter affects how the circuit is optimized. Here's what each level does:

1. **`optimization_level=0`**: No optimization is applied. The circuit remains unchanged.

2. **`optimization_level=1`**: Basic optimizations are performed, such as decomposing multi-qubit gates into single-qubit gates and canceling adjacent gates¹.

3. **`optimization_level=2`**: In addition to level 1 optimizations, it further simplifies the circuit by canceling out gates that can be combined³.

4. **`optimization_level=3`**: This is the highest level. It uses smarter algorithms to optimize the circuit, including additional gate cancellations and other advanced techniques¹. However, keep in mind that higher optimization levels may require more computational effort.

Choose the appropriate level based on your specific requirements and the trade-off between optimization and computation time. 😊

Source: Conversation with Copilot, 7/20/2024

We put in 1 phase change unit of pi/4. For a complete rotation, that is 8. We

got out 1/2^3 (on three qubits), which is 1/8...