QuantumInfo_Lesson3

 Back to IBM learning; silly me, I gave up on lesson3 just when the explanation

of inner product was about to get simple. One can appreciate the whole thing from

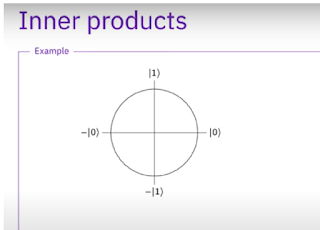
a simple diagram in 2-d which represents a qubit. We are not on the Bloch sphere at all...

                                                          

The notion of Euclidian Norm, however, does come from Born's rule in Quantum

Mechanics. Below, Copilot:

In quantum mechanics, the Euclidean norm plays a crucial role in representing quantum states. Let's delve into this! 😊

1. **Quantum States and Hilbert Space:**

   - Quantum states are represented by vectors in a Hilbert space. This space can be finite- or infinite-dimensional and is defined over complex numbers.

   - A quantum state is essentially a **ray** in this Hilbert space. Rays represent equivalence classes of vectors pointing in the same direction.

   - While these states are not necessarily normalized (i.e., unit vectors), it's more convenient to work with normalized states.

2. **Born's Rule and Probability:**

   - Born's rule connects quantum states to probabilities. It states that the probability of finding a quantum system in state |x⟩ after measurement is given by |ψ(x)|².

   - To ensure that the sum (or integral) of probabilities over all possible states equals 1, we normalize the states.

   - The normalization involves taking the square root of the sum or integral: √∑x |ψ(x)|² = 1 or √∫|ψ(x)|² dx = 1.

   - Remarkably, this normalization corresponds to the **Euclidean norm** (also known as the L²-norm).

3. **Why the Euclidean Norm?**

   - The Euclidean norm (2-norm) emerges naturally due to Born's rule, which is a fundamental postulate of quantum mechanics.

   - Other norms (such as p-norms with p > 2) wouldn't be as useful because they wouldn't satisfy the necessary homogeneity property.

   - In summary, the Euclidean norm's special status arises from its connection to Born's rule and the probabilistic interpretation of .

(2) Quantum states are unit vectors... with respect to which norm?. https://quantumcomputing.stackexchange.com/questions/2729/quantum-states-are-unit-vectors-with-respect-to-which-norm.

(3) L^2-Norm -- from Wolfram MathWorld. httquantum states.

For more mathematical details, you can explore the concept of norms in vector spaces [here](https://ai.stanford.edu/~gwthomas/notes/norms-inner-products.pdf) ². If you have any further questions, feel free to ask! 🌟

Source: Conversation with Copilot, 8/3/2024

(1) Norms and Inner Products - Stanford University. https://ai.stanford.edu/~gwthomas/notes/norms-inner-products.pdfps://mathworld.wolfram.com/L2-Norm.html.