Been pondering Riemann's first statement. That
sentence with the Euler equation has no verb; the
'is equal to' of the equation is the verb.
In point of fact, the Euler equation is an identity about
convergence. Taking an integral is a convergece test, but
not any old integral ( a lot of them go to zero!?) There
has to be some sense of adequacy (adéquation) between the two!
Tomorrow's problem!
* * *
In the light of day, Riemann's first paragraph asserts - no questions asked - that
the Euler identity holds for the complex plane, where the real part of x is greater
than 1. And let us note that the multiplication term, migrated to the left, is over
prime numbers; while the n on the right is over all whole numbers.
In effect, he talks about the two expressions as defining a unique
function of the variable x, whose commonality is that each converges
to a certain value (pi^2/6... not resolved to this day). But not always true.
The equation he proposes - with (s-1) to cover cases between zero and
one - is a promise to produce a finite-valued function over the
whole complex plane - excepting 1 - that is always true. He later claims to
have done so with:
It is a sine function, and its purpose will be to aid in dtermining the
number of primes at work up to a certain number.
* * *
I am being unfair to B. Riemann here; he is merely
trying to save the situation. By the time of this paper,
Euler's initial work on zeta was fifty years old, and quite
a bit of work had been done on the notion limits and the
uses of integration. Mathematics had also moved on to
group theory, looking at solability generally... Between Euler
and Rieman were Gauss, Dirichlet, Jacobi in Germany; Cauchy
in France.
But it remains euristhically useful to apprehend that he is
leading to what can be usefully said on the topic for his time:
how to pace convergence. Interestingly, Riemann will look to
the presence of primes in the unrolling numbers series. And
for us, those zeros in the complex case are not incudental!




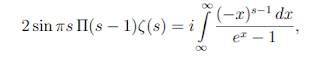
No comments:
Post a Comment