So what is the situation, here. From Calculus, the truth of
integration is established because it represents the addition
of many smaller values ie a series. So in this instance, a series
is represented by its integral, from negative to positive
infinity.
On the left side, we are on the complex plane, which is cyclical
for 2pi.
The function is sine, so the imginary component. It is a function
s on x, which gives a y value, effectively i.
There is an i constant which preceeds the integration on the right.
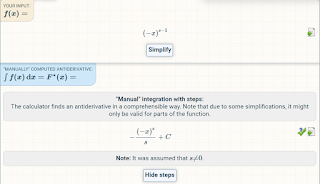
Integrating (-x) yields an i value, which is negative. Which comes to -(-1).
The function produces initial positive values, as expected.
The term to be integrated is over (e^x)-1, always modest. Zero comes in at 1.
* * *




No comments:
Post a Comment