Orientation

 Tomorrow will be the first day of Spring; in the Northern hemisphere, we

use the term Vernal Equinox for the cross-over, this year at 11pm Eastern Time.

Just had to ask about this; I've been confused for years about how our position in 

the solar system matches onto our position within the Milky Way. 60 degrees inclined,

but how does this all look on the same visual. PerplexityAI came through with the 

following:

                                                      

From Wikipedia, the ecliptic (apparent movement of the Sun in the sky):

                                         

                                                                              

         

                                                                      *     *     *

From Bing/Chat:

You

Mathematics; how many degrees does a triangle on a sphere have.

Copilot

Certainly! Let’s explore the fascinating world of spherical triangles. Unlike planar triangles, which exist on a flat surface, spherical triangles are formed on the curved surface of a sphere. Here are some intriguing properties:

Angle Sum: The sum of the angles in a spherical triangle is greater than 180 degrees. In fact, it can range between 180 degrees and π radians (approximately 3.14 radians)12. This deviation from the familiar Euclidean geometry is due to the curvature of the sphere.

Congruence: Two spherical triangles with the same angles are not just similar; they are congruent! This means that if you have two spherical triangles with identical angle measurements, they will have the same shape and size, regardless of their position on the sphere3.

Spherical Excess: Let’s denote the angles of a spherical triangle as A, B, and C (measured in radians along the surface of the sphere). The excess of the sum of these angles over 180 degrees (or π radians) is called the spherical excess. Mathematically, it’s given by: [ \text{Spherical Excess} = (A + B + C) - \pi ] The spherical excess is directly proportional to the surface area of the spherical triangle2. So, the larger the excess, the larger the triangle’s area.

Inner and Outer Triangles: Any spherical triangle can be considered both an inner and an outer triangle. If the three connecting arcs form two triangles—one taking up each hemisphere—then they are equal in size. However, in general, one triangle will be larger than the other. The inner triangle is usually assumed for calculations1.

In summary, spherical triangles exhibit intriguing properties due to the curvature of the sphere, and their angles defy the rules of planar geometry. Exploring these concepts leads us into the captivating realm of spherical trigonometry! 🌐🔍

                                                                          *     *     *

You

Is the Galactic Coordinate System spherical

Copilot

Certainly! The galactic coordinate system is indeed a celestial coordinate system that uses spherical coordinates. Let’s delve into its fascinating properties:

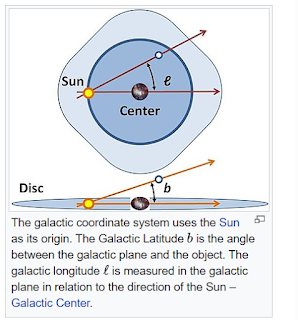
Definition: The galactic coordinate system centers around the Sun as its origin. The primary direction aligns with the approximate center of the Milky Way Galaxy, and the fundamental plane is parallel to an approximation of the galactic plane, albeit slightly offset to the north12.

Spherical Coordinates:

Galactic Longitude (l): Measured along the galactic equator from the Galactic Center, analogous to terrestrial longitude. It is usually expressed in degrees (°).

Galactic Latitude (b): Measures the angle of an object above the galactic plane (or midplane) as viewed from Earth. Similar to terrestrial latitude, it is also measured in degrees (°)1.

Historical Context:

The first galactic coordinate system was introduced by William Herschel in 1785.

Over time, various coordinate systems were used until 1932, when Lund Observatory established a standard system based on a galactic north pole at RA 12h 40m, dec +28° (in the B1900.0 epoch convention) and a 0° longitude where the galactic plane intersects the equatorial plane.

In 1958, the International Astronomical Union (IAU) redefined the system based on radio observations of galactic neutral hydrogen, adjusting the Galactic longitude by 32° and the latitude by 1.5°1.

Coordinate Details:

The north galactic pole (for equinox and equator of 1950.0) lies at right ascension 12h 49m, declination +27.4° in the constellation Coma Berenices.

Galactic longitude increases in the same direction as right ascension.

Galactic latitude is positive toward the north galactic pole, with the plane passing through the Sun and parallel to the galactic equator being 0°, while the poles are ±90°1.

In summary, the galactic coordinate system is indeed spherical, and its unique properties allow astronomers to navigate the vast expanse of our Milky Way Galaxy! 🌌🔭🌟